Senin, 03 Januari 2011

ALGORITMA PENCARIAN

Pencarian Biner

Pencarian Biner dilakukan untuk :
  • memperkecil jumlah operasi pembandingan yang harus dilakukan antara data yang dicari dengan data yang ada di dalam tabel, khususnya untuk jumlah data yang sangat besar ukurannya.
  • Prinsip dasarnya adalah melakukan proses pembagian ruang pencarian secara berulang-ulang sampai data ditemukan atau sampai ruang pencarian tidak dapat dibagi lagi (berarti ada kemungkinan data tidak ditemukan).
  • Syarat utama untuk pencarian biner adalah data di dalam tabel harus sudah terurut, misalkan terurut menaik.


ALGORITMA  

Kamus
      Const N : integer = 8  { misalkan jumlah elemen array maksimum = 8 }
      Type A = array [ 1 ..... N ] of integer
      Cari, BatasAtas, BatasBawah, Tengah : Integer
      Ketemu : boolean
ALGORITMA
         Input (cari) { meminta nilai data yang akan dicari}
         BatasAtas     ¬  1 { indeks array dimulai dari 1 }
         BatasBawah     ¬   N    
         Ketemu   ¬  False
         While (BatasAtas < BatasBawah) and (not ketemu) do
               Tengah ¬   (BatasAtas  + BatasBawah) div 2
               If A [Tengah] = cari then
                  Ketemu ¬ true
                           Else
                                 If ( A [Tengah]  < cari ) then { cari di bagian kanan }
                                       BatasAtas ¬ Tengah + 1
                                 Else
                                       BatasBawah ¬ Tengah – 1 { cari di bagian kiri }
                                 Endif
                           Endif
         EndWhile
         If (ketemu) then
                     Output ( ‘Data berada di index nomor’, Tengah )
         Else     Output ( ‘Data tidak ditemukan’ )
         Endif

Pencarian Sekuensial

“Sequential search atau Pencarian sekuensial” bisa disebut dengan pencarian linear yang merupakan model pencarian yang paling simpel dan sederhana banget deh yang dapat dilakukan terhadap suatu kumpulan data. Suatu tekhnik pencarian dalam array (1 dimensi) yang akan menelusuri semua elemen-elemen array dari awal sampai akhir, dimana data-data tidak perlu diurutkan terlebih dahulu.

Biar kalian lebih paham secara konsep, penjelasannya adalah sebagai berikut :
Keunggulan dari pencarian sekuensial ini adalah jika data yang dicari terletak di indeks array terdepan maka waktu dalam pencarian nya sangat cepat, dalam artian waktu yang minim sekali. Keburukannya adalah kalau jika data indeks array nya yang dicari paling belakang, maka waktu yang dicari tuh lama banget (maksimal).

Terdapat L yang merupakan larik yang berisi n buah data ( L[0],L[1]…….L[n-1]) dan k adalah data yang akan dicari. Pencarian dilakukan untuk menemukan L[i] = k dengan i adalah bilangan indeks terkecil yang memenuhi kondisi 0<= k <=n-1. Tentu saja bahwa data yang di cari tidak ditemukan.
Jika misalnya terdapat angka 4, maka ditulis ada, sedangkan jika dimunculkan angka 6, namun angka 6 tidak ada maka akan muncul tulisan tidak ada.
Berikut merupakan program yang telah dibuat sebelumnya :

L = {4,12,9,-2,12,7,1,100}

Tahukah kamu dimana posisi 12 yang pertama ?

Nah, dalam hal ini k adalah 12 dan k ditemukan berupa indeks 2. Angka 12 yang pertama akan dipilih oleh program, karena secara logika angka 12 merupakan data yang pertama muncul. Coba deh kamu bayangin aja misalnya dalam antrian, orang yang mengantri di depan akan duluan mendapatkan giliran. 
contohnya :

//Sequential searching
#include
#include
void main()
{
clrscr();
int data[8] = {4,12,9,-2,12,7,1,100};
int cari,index;
int ketemu=0;
cout<<"masukkan data yang ingin dicari = ";
cin>>cari;
for(int i=0;i<8;i++)
{
if(data[i] == cari)
{
ketemu=1;
index = i;
break;
}
}
if(ketemu == 1)
{
cout<<"Data ada!"<
cout<<"Data terletak di index ke - "<
}
else cout<<"Data Tidak ada!"<
getch();
}
 
pencarian string
 

Algoritma pencarian string atau sering disebut juga pencocokan string adalah algoritma untuk melakukan pencarian semua kemunculanstring pendek pattern[0..n − 1] yang disebut pattern di string yang lebih panjang teks[0..m − 1] yang disebut teks.
Pencocokkan string merupakan permasalahan paling sederhana dari semua permasalahan string lainnya, dan dianggap sebagai bagian daripemrosesan data, pengkompresian data, analisis leksikal, dan temu balik informasi. Teknik untuk menyelesaikan permasalahan pencocokkan string biasanya akan menghasilkan implikasi langsung ke aplikasi string lainnya.

Contoh algoritma pencocokkan string

Algoritma-algoritma pencocokkan string dapat diklasifikasikan menjadi tiga bagian menurut arah pencariannya.
Tiga kategori itu adalah :
  • Dari arah yang paling alami, dari kiri ke kanan, yang merupakan arah untuk membaca, algoritma yang termasuk kategori ini adalah:
    1. Algoritma Brute Force
    2. Algoritma dari Morris dan Pratt, yang kemudian dikembangkan oleh Knuth, Morris, dan Pratt
  • Dari kanan ke kiri, arah yang biasanya menghasilkan hasil terbaik secara praktikal, contohnya adalah:
    1. Algoritma dari Boyer dan Moore, yang kemudian banyak dikembangkan, menjadi Algoritma turbo Boyer-Moore, Algoritma tuned Boyer-Moore, dan Algoritma Zhu-Takaoka;
  • Dan kategori terakhir, dari arah yang ditentukan secara spesifik oleh algoritma tersebut, arah ini menghasilkan hasil terbaik secara teoritis, algoritma yang termasuk kategori ini adalah:
    1. Algoritma Colussi
    2. Algoritma Crochemore-Perrin

Algoritma brute force dalam pencarian string

Algoritma brute force merupakan algoritma pencocokan string yang ditulis tanpa memikirkan peningkatan performa. Algoritma ini sangat jarang dipakai dalam praktek, namun berguna dalam studi pembanding dan studi-studi lainnya.

Cara kerja

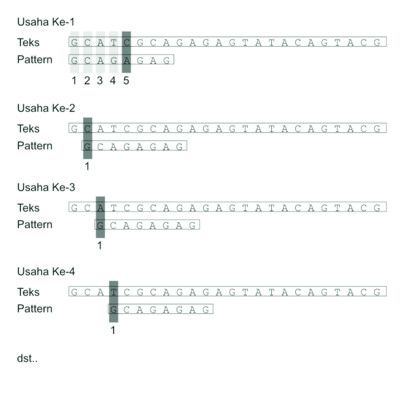
Secara sistematis, langkah-langkah yang dilakukan algoritma brute force pada saat mencocokkan string adalah:
  1. Algoritma brute force mulai mencocokkan pattern pada awal teks.
  2. Dari kiri ke kanan, algoritma ini akan mencocokkan karakter per karakter pattern dengan karakter di teks yang bersesuaian, sampai salah satu kondisi berikut dipenuhi:
    1. Karakter di pattern dan di teks yang dibandingkan tidak cocok (mismatch).
    2. Semua karakter di pattern cocok. Kemudian algoritma akan memberitahukan penemuan di posisi ini.
  3. Algoritma kemudian terus menggeser pattern sebesar satu ke kanan, dan mengulangi langkah ke-2 sampai pattern berada di ujung teks.
Berikut adalah gambar Algoritma brute force yang sedang bekerja mencari string:

ini psikodotnya

01<pre>procedure BruteForceSearch(
02        input m, n : integer,
03        input P : array[0..n-1] of char,
04        input T : array[0..m-1] of char,
05        output ketemu : array[0..m-1] of boolean
06       )
07
08Deklarasi:
09       i, j: integer
10
11Algoritma:
12        for (i:=0 to  m-n) do
13               j:=0
14               while (j < n and T[i+j] = P[j]) do
15                        j:=j+1
16               endwhile
17               if(j >= n) then
18                 ketemu[i]:=true;
19               endif
20        endfor
Diposting oleh di

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)